29 Mar 2020 Notes on Derivative Valuation and Illiquid Assets
These notes record some partially developed thoughts on how the presence of asset illiquidity and an illiquidity premium can theoretically impact on the relative valuation of liquid and illiquid derivative assets of illiquid assets. An appendix then discusses the theoretical implications for the valuation of equity release mortgages.
This is a potentially difficult and confusing topic. If we specify that an illiquidity premium is applied in the valuation of illiquid assets, we must be clear what we mean by liquid and illiquid, i.e. what conditions are necessary in order for the asset to have the property of being liquid or illiquid. For example, does it mean that trading the asset incurs a transaction cost above some particular level, or that there is a market price impact of selling a given volume of the asset? Virtually all assets will incur some transaction costs in trading them; and there will be some level of volume of transaction at which there will be some market price impact for virtually any asset. So perhaps no physical or financial asset is really perfectly liquid (except cash). Similarly, if an illiquid asset can be used as collateral to raise cash, perhaps such an asset can offer at least some liquidity.
And many complications immediately follow. Does the same illiquidity premium apply to all illiquid assets, irrespective of the riskiness of their cashflows? Does the illiquidity premium vary over time, and if so, is that variation correlated with market risk factors? And can these aspects of illiquidity behaviour be empirically measured in a reliable and accurate way?
These are interesting and challenging questions, but this note is not going to consider the empirical behaviour of the illiquidity premium, or even whether such a thing ‘really’ exists. Instead, we are going to consider a very abstract model that is focused on a particular sort of question: if an illiquidity premium does exist, how does this affect the prices of assets that are derivatives of an illiquid asset?
Standard option pricing theory is based on dynamic replication, and we will not consider here how illiquidity can be incorporated into that setting (though we note in passing that there is a long-established literature on option pricing when transaction costs are incurred in trading the underlying asset). This note will consider the simpler setting of derivatives that only require static replication. In particular, we will consider the case where a house meets the criteria of an illiquid asset. And we will consider a particular form of derivative asset where the house is the underlying asset: a deferment asset, which we define as the asset that gives the right and obligation to take ownership of the house at some specified future time t. (Note that an equity release mortgage is equivalent to the deferment asset on the house when it is known that the value of the house will be less than the mortgage loan balance at a known maturity date. More generally, the value of the deferment asset is an upper bound for the value of an equity release mortgage of the same liquidity.)
We will explore how to answer the following questions: if an illiquidity premium exists, and the house is an illiquid asset, then what is the value of the deferment asset? Is the value of a liquid deferment asset different to the value of an illiquid deferment asset, and if so how?
You may well question whether it is reasonable to suppose a liquid derivative asset on an underlying illiquid asset can exist. We are not going to consider that point here, we are only going to try to work through its implications if it were to exist (and it existed alongside a non-zero illiquidity premium).
To do this, we will start by postulating a radically simple abstract world, as follows:
1. Asset liquidity is a binary state: an asset is either liquid or illiquid. We specify that a liquid asset can be instantly converted into cash in unlimited volume at the asset’s market value without cost. That definition is quite straightforward (though we will see later that there is still a need to interpret just what this means when we write or sell a liquid asset). However, defining exactly what illiquidity means is harder. We could start by simply supposing an illiquid asset can never be sold. But then that implies the deferment asset (which entails the transfer of house ownership from one party to another) cannot exist. So here we will simply specify that illiquid assets do not have the liquidity properties of liquid assets and we will note that this isn’t an entirely satisfactory definition. In the analysis below, we will assume the illiquid asset can be purchased for cash at its market value at any time. But we will never assume the illiquid asset can be sold, except via the transfer of ownership that is delivered by the deferment asset. We will also specify that the liquid asset is always liquid (until it matures or expires, where applicable) and the illiquid asset is always illiquid (until it matures or expires, where applicable). And, finally, everyone knows which assets are liquid and which are illiquid.
2. We now introduce the concept of proceed-equivalence. We define proceed-equivalent assets as two assets that produce the same proceeds in all states of the world (these proceeds may be cashflows or other assets, and those assets may be liquid or illiquid). We specify that proceed-equivalent assets of the same liquidity ‘state’ (liquid or illiquid) must have the same market value.
3. All illiquid assets are valued with an equal and constant illiquidity premium relative to their liquid proceed-equivalent asset. That is, the proceeds of the illiquid asset are discounted at a rate λ higher than the discount rate applied to the proceeds of the proceed-equivalent liquid asset in all states of the world. This relationship applies to all assets, irrespective of the riskiness of the assets. If λ > 0 and the assets can only generate proceeds with positive values, then the market value of an illiquid asset is lower than the market value of its proceed-equivalent liquid asset (prior to maturity / expiry of the assets).
4. An asset called a house exists and it is an illiquid asset. We know it has a current market value, S. The house asset will generate income over the next t years such that the house provides a certain continuous income yield (as a percentage of its market value), d, over the next t years. We do not make any assumptions about the income generated by the house after time t.
5. We suppose another asset exists today that provides the holder of the asset with the contractual right and obligation to take ownership of the house at time t. We call this asset the deferment asset. The deferment asset may be liquid or illiquid. The deferment asset expires at time t and it generates one proceed: the house at time t.
We will argue that the five groups of premises above determine unique answers to the following questions: Given the presence of a positive illiquidity premium, what is the value of the deferment asset if it is liquid? And what is its value if it is illiquid? Below, we show how these unique answers can be determined if 1.-5. hold true.
The elephant in the room – arbitrage in a world with illiquidity
Before we do that, there is a potentially disturbing elephant in the room that may arise from premise 3. above: it directly implies that if we go long (short) any given illiquid asset, and short (long) its proceed-equivalent liquid asset, we will have constructed a portfolio that will generate net proceeds of zero at all times in all states of the world, and yet which has negative (positive) value today (because, by 3. above, the illiquid asset has a lower market value than its proceed-equivalent liquid asset when λ > 0).
For some, this immediate and obvious consequence of the above premises may seem too perverse to warrant any further consideration of their other logical implications. We certainly need to bottom out what this means before we proceed any further.
The first point to note is that the presence of a positive illiquidity premium directly implies that the market value of an asset depends not only on its cashflows but also on its liquidity state. A world with a positive illiquidity premium is a world where liquidity has an economic value. It is trivially obvious that a positive illiquidity premium implies that going long an illiquid asset and short an otherwise equivalent liquid asset of an equal market value creates positive net cashflows in all states of the world. If all assets are liquid, then this represents an unambiguous arbitrage. But here all assets are explicitly not liquid. The following discussion argues that this limits the availability of transactions in a way that removes the possibility of arbitrage.
Consider the case where we are long an illiquid asset and short the proceed-equivalent liquid asset. What does it mean to short a liquid asset? Shorting a liquid asset means creating a liquid liability. In this world, we will specify that shorting a liquid asset means giving your counterparty the option to sell the asset back to you for cash at any time (prior to expiry or maturity of the asset, where applicable) of the counterparty’s choosing at its then-prevailing market value[1]. It is this commitment that makes the asset liquid for your counterparty. On the other hand, if you short an illiquid asset, you create an illiquid liability and you have not granted your counterparty this liquidation option.
In the presence of a positive illiquidity premium, when you sell a liquid asset and create a liquid liability, you receive more cash than you would have if you were to sell an illiquid asset and create an illiquid liability. In such a scenario, your counterparty (or regulator, etc.) would naturally require you to be able to make good on the service that you have charged a price for – i.e. granting the counterparty the right to sell the asset back to you instantly for cash at market value at any time of their choosing. Perhaps, for example, the counterparty would require you to put the required amount of liquid assets in an escrow account. Whatever the ‘liquidity collateralisation’ mechanism, the creation of a liquid liability creates a requirement for the bearer of the liability to hold assets in liquid form. If you did not have this liquid liability obligation, those liquid assets could be invested in illiquid assets that would earn the illiquidity premium.
Hence, in a world with a positive illiquidity premium, creating a liquid liability (as opposed to an illiquid liability) constrains the asset side of the balance sheet, and this creates an opportunity cost: by creating a liquid liability, you create a requirement to hold assets in liquid form that could otherwise been invested in illiquidity premium-earning illiquid assets. The economic value of this opportunity cost is the difference in value between the liquid and illiquid asset.
This explains why a zero net cashflow position that is net short liquidity has negative market value in a world with a positive illiquidity premium. The creation of a liquid liability creates a necessity to hold liquid assets to back it. Put another way, if all your assets are illiquid, it is simply not possible to sell a liquid asset, because you do not have liquidity to sell.
Now let’s consider the case where we are long a liquid asset and short the proceed-equivalent illiquid asset. According to our postulate 3., such a position will have a positive market value today, even though it will produce zero net cashflows at all times. Does this make sense? Yes – when in this position, the illiquidity of the short position gives us the option to sell our liquid assets and invest the cash in higher-yielding illiquid assets. These assets will then generate certain excess cashflows over the cashflows produced by the liquid asset’s proceed-equivalent illiquid asset (which, in this case, is our liability). These certain excess cashflows have a positive economic present value, and this is the difference between the market value of the liquid asset and the market value of the proceed-equivalent illiquid asset.
Let’s bring this point to life with a very simple example. Suppose the interest rate is 2% and the illiquidity premium is 1% and we hold a liquid asset that will pay a cashflow of 1 in one year. Its market value today is therefore exp(-0.02) = 0.98. And further suppose we are short a 1-year illiquid loan, which means we must pay a cash amount of 1 in one year. According to the above postulates, this illiquid loan has a market value of exp[-(0.02+0.01)] = 0.97. In all states of the world, this portfolio will produce a single net cashflow of 0 after 1 year. And yet it has a positive market value. Why? Because we have a liquidity surplus. The illiquidity of our liability allows the liability cashflow to be replicated more cheaply than if it was liquid. We can therefore sell the liquid asset for 0.98 and buy 0.98 of illiquid asset, because we have no need for the liquidity as the liability is illiquid. This illiquid asset will have a pay-off of 0.98.exp(0.02+0.01) = 1.01. So, by monetising our liquidity surplus, we have constructed a certain net cashflow of 1.01 – 1 = 0.01. This is why a positive illiquidity premium implies that a zero net cashflow position that is long liquidity must have positive market value. Being long a liquid asset and short a proceed-equivalent illiquid asset is, in the presence of a positive illiquidity premium, economically equivalent to being long more illiquid asset than you are short.
The above arguments imply that all balance sheets will maintain a zero net liquidity position. If there is any excess positive liquidity on the balance sheet, this excess will be monetised by selling some liquid assets and buying illiquid assets. And it will not be possible to maintain a net negative liquidity position because the creation of a liquid liability will create a requirement to hold a corresponding amount of liquid assets (in order to deliver on the liquidity option that you have granted to the liability counterparty by agreeing to write them a liquid rather than illiquid asset).
The presence of an illiquidity premium directly implies that a zero net cashflow portfolio that is net long (short) liquidity must have positive (negative) market value. Arguing that a zero net cashflow portfolio must have zero market value irrespective of the liquidity of its assets and liabilities is just another way of saying the illiquidity premium must be zero. As per the introductory paragraphs above, this note does not consider whether an illiquidity premium ‘really’ exists or not. It is analysing the valuation implications if an illiquidity premium does exist. The above arguments suggest that if we recognise the natural asset investment constraints that must be associated with the creation of liquid liabilities, liquidity can conceptually be a factor of the valuation function of assets without creating arbitrage between liquid and illiquid assets.
Valuing the deferment asset
Let’s now return to our question of how to value the deferment asset in its liquid and illiquid state. To simplify the discussion, we will start with the assumption that d = 0. Recall d is the continuous income yield of the house, as a percentage of its market value, between now and time t. We make no assumption about the nature of the house income after time t.
We’ll start with the deferment asset in its illiquid form. In this case, the valuation of the deferment asset is quite trivial. The deferment asset and the house have the same illiquidity state (both illiquid). If d = 0, then the deferment asset will generate identical proceeds to the house: that is, both assets generate zero cashflows between now and time t, and at time t the deferment asset holder becomes the house owner and hence will consequently participate in whatever income the house produces after time t in exactly the same way as they would if they were the house owner today (note this does not require any assumption about what income will be paid by the house after time t, and we have not made any assumptions about this in this analysis).
Therefore, we have two proceed-equivalent assets with the same liquidity state (both the house and the deferment asset are illiquid), and by 2. above the assets therefore have the same market value. And so, when d = 0, the current market value of the illiquid deferment asset is the current market value of the house, S.
Now consider the liquid deferment asset. Unlike the illiquid deferment asset, the holder of the liquid deferment asset can convert the deferment asset’s market value into cash at any time up until time t. Note the deferment asset (and, hence, its liquidity) expires at time t. That is, at time t, the holder of the liquid deferment asset becomes the owner of the illiquid house, and the past liquidity of the deferment asset is from that point irrelevant. Hence, for t = 0, the liquid asset value must be equal to the house value (and equal to the illiquid deferment asset value).
For t > 0, we can observe that the liquid deferment asset will generate the same proceeds as the illiquid deferment asset in all states of the world: the two assets generate no proceeds between now and time t, and at time t the holders of these assets will both receive the house asset. The liquid and illiquid deferment assets are therefore proceed-equivalent as per our definition in 2. above, and the assets expire at time t. We can therefore invoke premise 3. to deduce that, when d = 0, the current market value of the liquid deferment asset = exp(lt) x Illiquid deferment asset value = S.exp(λt).
Let’s pause and consider this result. This says that, in the presence of a positive illiquidity premium, the liquid deferment asset is more valuable than both the illiquid deferment asset and the house, even though all three assets have exactly the same proceeds in all states of the world. Why would this be the case? The holder of the liquid deferment asset has the option to convert the economic value of their exposure to the illiquid house into cash between now and time t, and this is an option that the illiquid deferment asset owner and the (illiquid) house owner do not have. In a world with a positive illiquidity premium, this option has a positive economic value.
But there is an interesting counter-argument to this….why can’t the house owner create immediate liquidity by writing an illiquid deferment asset on the house? This is equivalent to using the house as collateral to borrow cash (and this is of course exactly what an equity release mortgage does). The existence of such an option implies the illiquid house is perhaps not so illiquid after all. But the house owner can only use the house as collateral on one loan at a time. If a liquid deferment asset written on the house already exists (which we presume is the case if we are interested in valuing it), it implies there would at least be some limit to how much more deferment asset could be written by the house owner, and hence how much liquidity the house owner could extract from the house asset at the current time. Nonetheless, this point highlights the difficulty (for me at least!) in defining exactly what liquidity and illiquidity do and do not mean.
Now let’s relax our assumption that d = 0. If d > 0, then the house will pay a series of cashflows between now and time t. The deferment asset will not receive these cashflows (irrespective of whether the deferment asset is liquid or illiquid). Let’s consider how this impacts on the illiquid deferment asset first. The deferment asset receives the house at time t and nothing before then. So, the only difference between the proceeds of the deferment asset and the proceeds of the house is the income stream that is received by the house owner between now and time t. And the illiquid deferment asset has the same liquidity state as the house (i.e. illiquid). Therefore, the illiquid deferment asset value must be equal to the house value less the present value of the income stream received by the house owner between now and time t.
If the continuous income yield is a constant proportion of the market value of the house, then it is straightforward to show that the present value of this income stream is S[1-exp(-dt)]. Moreover, the present value of this income stream is not a function of the size of the illiquidity premium: as the income is expressed as constant percentage of the house value, a higher illiquidity premium implies higher expected income growth (because the house value grows more quickly over time as the illiquidity premium increases, and the income is assumed to be a constant proportion of this house value); and a higher illiquidity premium also implies a higher discount rate is applied to this higher income (as it belongs to an illiquid asset). The illiquidity premium cancels out in the calculation of the present value of future dividends just like it does for a house price risk premium.
But wait…if the present value of the dividends is not a function of the illiquidity premium, and the house is nothing more than the present value of all future dividends, how can this be squared with the idea that the illiquidity premium impacts on the value of the house? Because here we are already given the current value of the illiquid house, S. If the illiquidity premium changed, we would, of course, expect the value of the illiquid house to change. But given the illiquid house value, we don’t need to know the size of the illiquidity premium to assess the present value of income generated by the house (at least not when the income is a constant proportion of the house value).
This argument applies to the illiquidity premium in exactly the same way that it applies to the risk premium – the house value will vary with changes in the house risk premium but, given the value of the house, we do not need to know the risk premium in order to calculate the present value of any portion of the house’s income stream. This applies to the illiquidity premium in the same way: the market value of the illiquid house varies with the size of the illiquidity premium, but, given the current market value of the illiquid house, we do not need to know the illiquidity premium in order to calculate the present value of any portion of its income stream (at least when the income yield is a constant proportion of market value and the current market value is known).
So, the illiquid deferment asset value is equal to the house price less the present value of dividends =
S – S(1-exp(-dt)) = S.exp(-dt)
The liquid and illiquid deferment assets remain proceed-equivalent assets as they both produce one proceed, the house at time t, irrespective of the size of d. And so, by premise 2. above, the relationship liquid deferment asset = exp(λt) x Illiquid deferment asset value still applies when d > 0. We therefore obtain: liquid deferment asset = exp(λt) x S. exp(-dt) = S.exp[-(d-λ)t].
That is, the deferment rate that applies to a liquid deferment asset when the underlying asset is illiquid is the income yield less the illiquidity premium.
Concluding Thoughts
This note documents some exploratory thoughts on the valuation of liquid and illiquid derivative assets of an illiquid underlying asset, in the case where the derivative only requires static (rather than dynamic) replication. Some premises have been used to logically derive relationships that have been previously documented in recent Equity Release Mortgages research such as Jeffery & Smith (2019). We have argued that these premises are collectively sufficient to obtain the result that the income yield should be netted down by the illiquidity premium when valuing a liquid deferment asset on an illiquid underlying asset. Of course, there may be other quite different sets of premises that are also sufficient to obtain this result (that is, the premises specified in this note may not be necessary).
The above analysis presented in these notes, even as a simplified abstraction, is far from complete. In particular, the definitions of liquidity and illiquidity that have been used here are not fully developed. So, it is certainly not being suggested here that the rough sketch presented in this note constitutes an adequate formal model of the theoretical impact of illiquidity on derivative asset values. But the analysis suggests a fundamentally intuitive and indeed virtually tautological result: if a positive illiquidity premium exists, then liquid derivative assets will have a higher market value than illiquid derivative assets.
This note has not considered whether it is empirically reasonable to assume an illiquidity premium exists, or what size it may be, or whether it is reasonable to assume liquid deferment assets on illiquid underlying assets exist. It has merely considered what such conditions may logically imply for the relative pricing of a particular form of liquid and illiquid asset.
Appendix – More on ERM valuation and liquidity adjustments
The analysis developed above has been deliberately abstract and non-empirical. It has, however, highlighted that there are reasons for arguing houses are not perfectly illiquid (as they can be used as collateral to borrow cash; as well as the more obvious point that they do also change hands in a usually-functioning secondary market!); and there are reasons for arguing that equity release mortgages cannot be considered perfectly liquid (as the lender cannot demand cash settlement of the mortgage at any time of their choosing). Of course, one of the rationales for insurance firms investing in equity release mortgages is that they are not perfectly liquid. Annuity writers have illiquid liabilities and, as noted above, such balance sheets will naturally seek to monetise their excess liquidity when in the presence of a positive illiquidity premium.
So, to the extent that mortgages are more liquid than houses, the above analysis might provide some intuition for why and how a house illiquidity premium increases the mortgage value relative to the case where the mortgage and the house have the same liquidity; meanwhile, the presence of a loan illiquidity premium would reduce the value of the mortgage (and increase its expected return) to the extent that the mortgage asset is less than perfectly liquid.
The essential point is that equity release mortgages are valued with reference to the value of two key assets: a (quite illiquid) house and (a quite liquid) risk-free bond. A mortgage can perhaps (though not necessarily) be viewed as more liquid than the house and less liquid than the risk-free bond. If a positive illiquidity premium exists, allowances for the liquidity differentials between the mortgage and each of those reference assets are theoretically required in the mortgage valuation. Moreover, the impacts of these liquidity differentials will depend on the ‘moneyness’ of the no-negative equity guarantee (NNEG) of the mortgage. The impact of allowing for the effect of house illiquidity will be greater when the NNEG is likely to ‘bite’ (all else being equal). That is, deducting the house illiquidity premium from the deferment rate will have a greater impact on the mortgage value when LTV is higher (all else equal). Conversely, if it is certain that the NNEG will not bite, the NNEG is worth zero, and the house price illiquidity premium is irrelevant to the value of the mortgage. In such a situation, the mortgage is a risk-free loan, and the only liquidity effect will be the reduction in mortgage value that arises as a result of the mortgage being less liquid than the risk-free bond (i.e. the loan illiquidity premium).
These different illiquidity valuation effects can be qualitatively summarised by the following chart:
Chart 1: The Qualitative Impact of Liquidity Adjustments on Mortgage Value (in the presence of positive illiquidity premia)

Let’s now bring these qualitative dynamics to life with a highly simplified quantitative example. Suppose we write an ERM today with a known maturity in 25 years. The house has a current value of 1, the LTV is 30%, and so the loan amount is 0.3. The risk-free rate is 1.5% and the roll-up rate of the mortgage is 4.0% (and so the loan balance at maturity in 25 years is known to be 0.80). If we assume a house price volatility of 16% and a deferment rate of 3.5%, and make no allowance for illiquidity, we obtain a loan value of 0.33 (using Black-Scholes, the NNEG is 0.22 and the pre-NNEG value is 0.55).
Now let’s introduce some illiquidity premium impacts. We will suppose that a positive illiquidity premium exists. For simplicity, we will assume the house is illiquid and the risk-free asset from which the 1.5% interest rate is derived is liquid. For simplicity, we will assume that the illiquidity premium is 1%, and the same illiquidity premium applies to all illiquid assets (this isn’t suggesting 1% is or is not a reasonable estimate of the illiquidity premium, it is just an easy number to work with for illustration).
We need to know how the liquidity of the mortgage compares with the liquidity of the house and the liquidity of the risk-free asset in order to make the correct liquidity adjustments in the mortgage valuation. To further our understanding of these liquidity adjustments, let’s consider the valuation adjustments produced by the two ‘boundary conditions’ of assuming the mortgage is as liquid as the risk-free asset; and assuming the mortgage is as illiquid as the house. If the liquidity of the mortgage is somewhere between that of the house and that of the risk-free asset, then the ‘correct’ liquidity adjustment will be somewhere within the range of valuations produced by these two ‘boundary conditions’.
When the mortgage is as liquid as the risk-free asset, the above analysis suggests the reasonable liquidity valuation adjustment is found by deducting the house illiquidity premium from the deferment rate in the NNEG valuation (though we should point out we did not consider the option valuation case in this note, but only the (simpler) deferment asset).
When we assume the mortgage is as illiquid as the house, no adjustment for the house illiquidity premium is required, but, in the presence of a positive illiquidity premium, we need to adjust the mortgage valuation to account for its illiquidity relative to the risk-free asset (the loan illiquidity premium adjustment). We will adjust for the mortgage illiquidity by adding the loan illiquidity premium to the risk-free rate that is assumed in the mortgage valuation (both in the NNEG component and the ‘pre-NNEG’ component of the cashflow). (We haven’t derived a rationale for this approach to allowing for the loan illiquidity premium in this note, and it merits further analysis, but for current purposes, we will use it for this illustration, and we also note it is the approach developed in Section 5 of Jeffery & Smith (2019)).
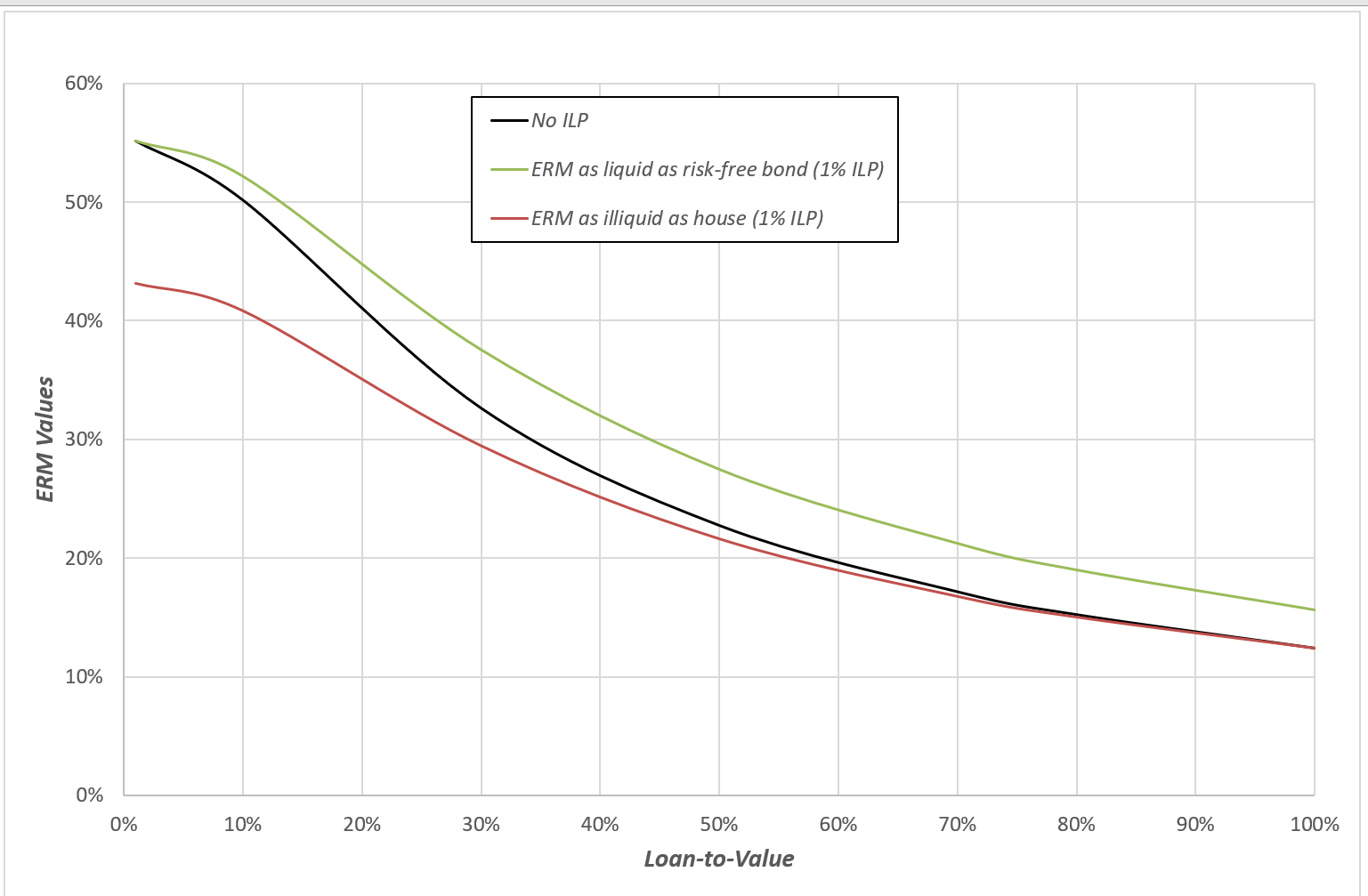
It is straightforward to produce the mortgage values that are produced by applying these valuation approaches to the two liquidity boundary conditions. The chart below shows the valuation results that are produced under the two ERM liquidity conditions and the value produced under a zero-illiquidity-premium case as the Loan-To-Value changes (by changing the starting house value and holding the loan amount of 0.3 fixed).
Chart 2: ERM Values (Liquid and Illiquid)

The black line above shows the ERM values that are produced when the illiquidity premium is zero. In this setting, the liquidity of the ERM is irrelevant to its value. The green line shows the ERM values produced by the assumption of the 1% house illiquidity premium when the mortgage is assumed to be liquid. The red line shows the ERM values produced by the assumption of the 1% loan illiquidity premium when the mortgage is assumed to be illiquid.
You can see that the quantitative liquidity valuation impacts of this example mortgage are consistent with the qualitative results of Chart 1. If the mortgage has liquidity somewhere between the liquidity of the risk-free asset and the liquidity of the house, the mortgage value should lie somewhere between the green and red lines for any given LTV. The two charts below plot the differences between the liquid and illiquid values and the no-ILP valuations.
Chart 3: ERM Liquidity Adjustments as % of no-ILP valuation (1% ILPs)
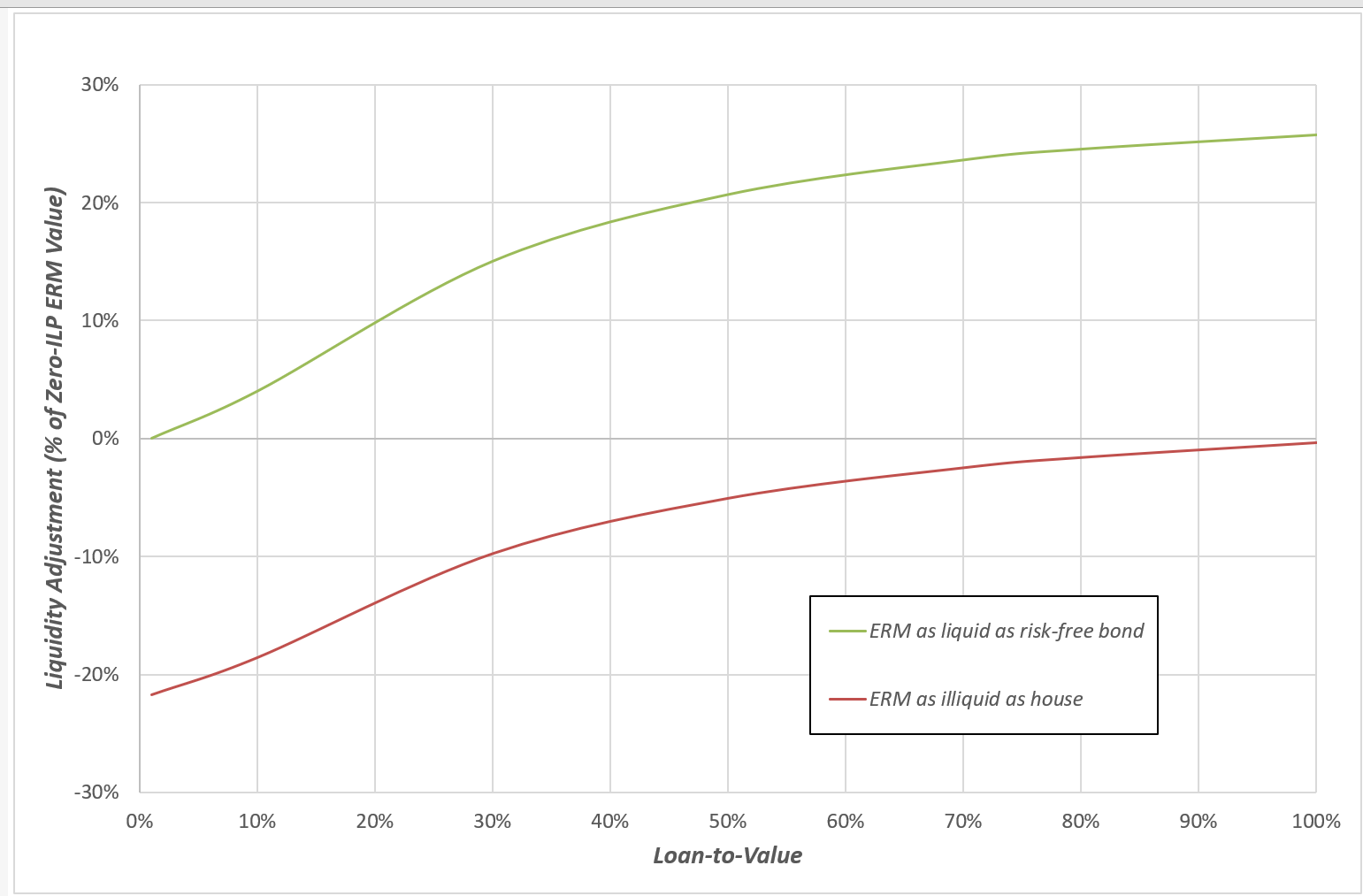
Chart 4: ERM Liquidity Adjustments (Difference between Liquidity Adjusted Value and no-ILP valuation (1% ILPs)
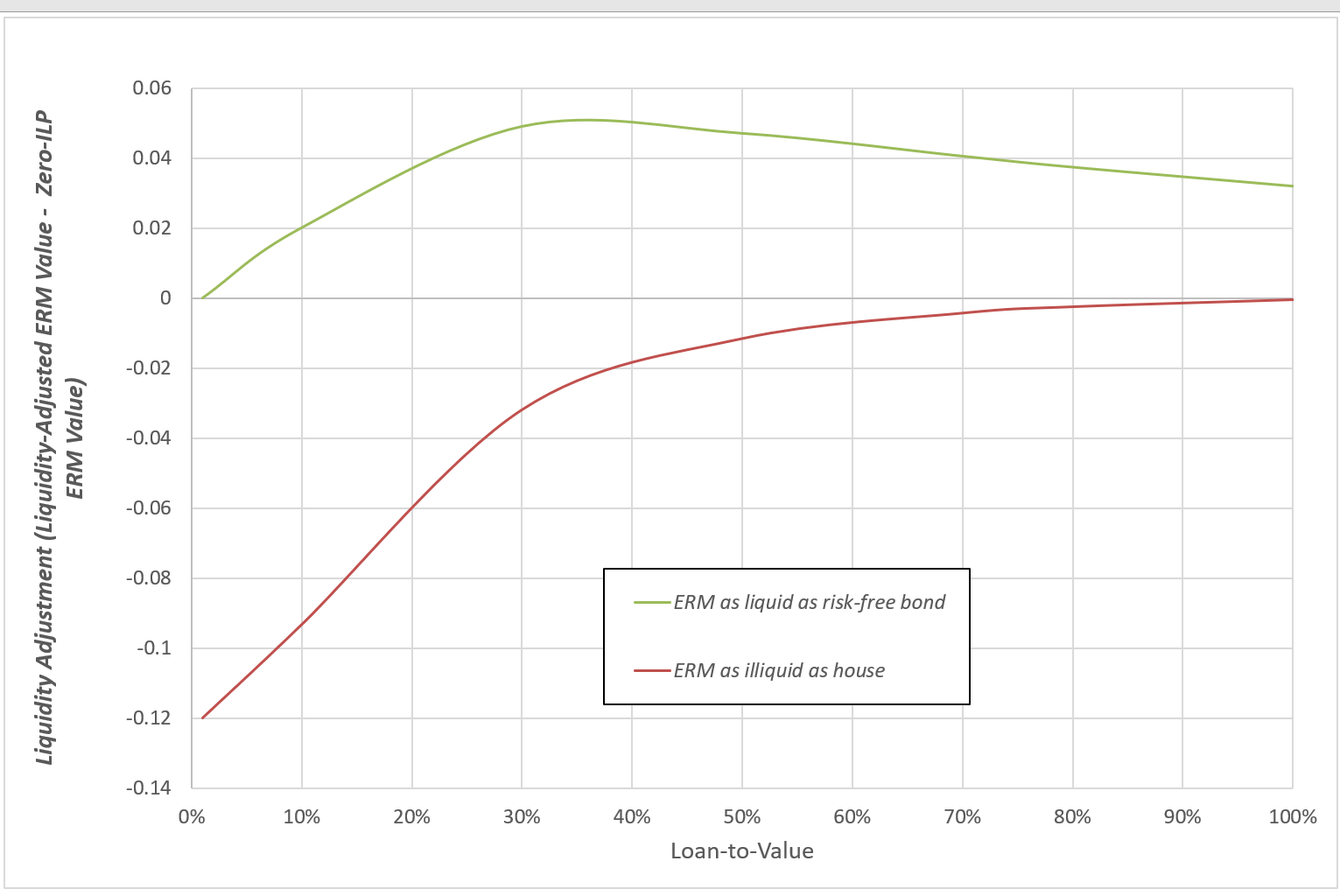
When the mortgage is liquid, its greater liquidity relative to the house results in a higher value for the mortgage when the illiquidity premium is positive. The percentage increase in mortgage value increases as the LTV of the mortgage increases (as the mortgage becomes more like the deferment asset and less like the risk-free bond). This percentage difference tends towards exp(λt) -1 = exp(1% x 25) -1 = 0.284 as LTV increases.
Likewise, when the mortgage is illiquid, the impact of the loan illiquidity premium increases as the LTV decreases. As the LTV tends to zero, the mortgage becomes a risk-free loan. If it has the same liquidity as the risk-free asset that has been referred to in the valuation, it has the same value as that asset. If it is less liquid than that asset, then the presence of a positive illiquidity premium produces a corresponding value reduction. As LTV tends to zero, this percentage difference tends towards exp(-λt) -1 = exp(-1% x 25) -1 = -0.221.
There is another important point that emerges from this analysis. Chart 3 shows that the % liquidity adjustment increases with LTV in the presence of a positive illiquidity premium. This is true for both the liquid and illiquid ERMs. This effect acts as a dampener on the valuation impact of house price falls. For example, if we start with a 30% LTV loan, and stress the house price down by 30%, the mortgage falls by 22% in the no-ILP case. In the presence of a 1% ILP, the fall in mortgage value is reduced from 22% to 19% (for both the liquid and illiquid ERMs).
These are highly simplified calculations that are simply intended to make the above qualitative discussion more accessible. The fundamental (empirical) question that this analysis raises is: how does mortgage liquidity compare with house liquidity (and risk-free asset liquidity)? This is the crucial question that determines how to make liquidity adjustments to the mortgage valuation in the presence of a positive illiquidity premium.
A Postscript on Illiquidity Premia and Equity Release Mortgage Valuation
To further illustrate the logic of these valuation effects, this postscript works through the valuation process for a single mortgage at the point of its origination, and highlights where this process is impacted by liquidity assumptions. The valuation at origination is interesting because we usually work with the additional constraint that the mortgage valuation at origination must equal the loan amount (we will ignore complications such as the treatment of acquisition costs). However, we may also note that in a valuation method that values the mortgage as the difference between the ‘pre-NNEG’ and NNEG cashflows, the origination valuation constraint does not directly constrain the size of these two valuation components, but only their difference.
To illustrate these effects, we will use an example mortgage with similar assumptions to those used above. The house is assumed to have a known value of 1 at the origination date. The risk-free interest rate is 1.5%. Our best estimates of the house price volatility and the house’s net income yield are 16% and 3.5% respectively. The mortgage has a fixed term of 25 years and a roll-up rate of 4.0%. The loan amount is 0.30. The ‘promised’ mortgage cashflow at maturity is therefore 0.80.
We will consider, in turn, the three valuation cases that were discussed above: where no illiquidity premium exists; where a 1% illiquidity premium exists and the mortgage is illiquid; where a 1% illiquidity premium exists and the mortgage is liquid.
Case 1: No Illiquidity Premium
The pre-NNEG cashflow of 0. 80 is risk-free and therefore has a present value of 0.80 / (1.015)^25 = 0.55.
Plugging our best estimates of net income yield and house price volatility into a Black-Scholes put option formula in the usual way produces a NNEG value of 0.22. We therefore obtain a mortgage value of 0.55 – 0.22 = 0.33.
The mortgage value of 0.33 is different to the loan amount of 0.30. Typical industry practice would explain this difference as a mortgage illiquidity valuation effect, but in this case we have explicitly ruled that out by assuming no illiquidity premium exists.
In such circumstances, the standard derivative valuation practice would be to adjust the underlying asset’s assumed volatility parameter so as to reconcile the valuation with its market value (the loan amount in this case). We can do that here. But before we do that, we should note that, unlike ‘conventional’ derivatives, the NNEG valuation uses two parameters are unobservable: the house price volatility and the net income yield. The net income yield is more opaque than, say, the dividend yield of an equity index. The net income yield estimate requires an estimate of the rental income that would be available on an owner-occupied house, as well as an estimate of the costs required to maintain that house. It is quite plausible that reasonable estimates of these quantities can be obtained, but it isn’t quite as simple as looking up the yield on a Bloomberg screen.
Moreover, the option pricing formula assumes the net income yield is constant through time. In reality, there may be material uncertainty in the net income yield of the house over the term of the mortgage. And, unlike may often be the case for an equity index, we have no easily observable forward prices that can tell us about the market value that is attached to the uncertain income stream (although, if we could observe some very high LTV mortgage values, that would give us a good clue).
So, the volatility and the net income yield parameters of the NNEG valuations may both be regarded as unobservable, and we could therefore be justified in adjusting either of our best estimates of these parameters to ‘mark’ the mortgage valuation to the loan amount at origination. In both cases, we need to adjust the parameter such that the value of the NNEG is increased from 0.22 to 0.25. This could be done by either increasing the assumed house price volatility from 16% to 19% or by increasing the assumed net income yield from 3.5% to 4.0% (or, indeed, some combination of the two).
Case 2: 1% Illiquidity Premium and an illiquid mortgage
In this case we assume there is a 1% illiquidity premium and the house is illiquid. As discussed above, here we need to adjust our mortgage valuation to reflect that we are referencing a liquid risk-free rate in the valuation when in fact we ought to be referencing the illiquid risk-free rate. So, we re-value both components of the mortgage value using the assumption that the relevant risk-free rate is the liquid risk-free rate (1.5%) plus the illiquidity premium (1%) = 2.5%.
The pre-NNEG value in this case is therefore 0.80 / (1.025)^25 = 0.43.
Plugging in our best estimate assumptions for house price volatility and net income yield into the Black-Scholes put option formula with a risk-free rate of 2.5% produces a value of 0.14. The calculated mortgage value is therefore 0.43 – 0.14 = 0.29.
This is clearly very close to our loan amount of 0.30, but some adjustment is still required to reconcile exactly. In this case, we arguably have three unobservable parameters that we could vary to ‘mark’ the valuation to the loan amount: the house price volatility, the net income yield of the house or the risk-free loan illiquidity premium. But it arguably would not make sense to fit the risk-free loan illiquidity premium assumption to the loan amount, as this would result in inconsistent (contradictory) risk-free loan illiquidity premia being assumed for different mortgage valuations at the same point in time. It therefore seems more natural to allow assumptions specific to the individual mortgage to vary.
If we take the illiquidity premium as given, then we are required to either reduce the house price volatility parameter from 16% t to 15%, or to reduce the net income yield from 3.5% to 3.35%.
Case 3: 1% Illiquidity Premium and a liquid mortgage
In this case the mortgage valuation process needs to adjust for the fact that we are referencing an illiquid house price in the valuation of a liquid mortgage. The analysis above argues that, under suitable assumptions, the way to adjust the mortgage valuation process for this effect is to reduce the estimated net income yield of the house by the house price illiquidity premium (which we assume here to be 1%). Hence the liquidity-adjusted deferment rate is 3.5% – 1% = 2.5%.
The pre-NNEG value here is the same as in Case 1: the mortgage is liquid, and so the value of the mortgage when it is risk-free is simply the promised cashflow discounted at the liquid risk-free rate. And so the pre-NNEG value is 0.55 as in Case 1.
If we now plug in our best estimate house price volatility parameter and our liquidity-adjusted net income yield of 2.5% into our usual Black-Scholes put option pricing formula, we obtain a NNEG value of 0.18. The mortgage value is therefore calculated to be 0.55 – 0.18 = 0.38.
As in Case 2, we might argue here we have three unobservable parameters: the house price volatility, the house’s net income yield and the house price illiquidity premium. Similarly to Case 2, we argue it would be difficult to assume different houses of the same illiquidity have very different illiquidity premia, and we therefore consider the changes in the house price volatility or (pre-liquidity-adjusted) net income yield that are required to obtain the NNEG of 0.25 that results in a ERM value at origination that is equal to the loan amount. The implied parameters required to obtain a mortgage valuation equal to the loan amount are a house price volatility of 24% or a net income yield of 5.0% (before illiquidity adjustment).
In Summary
Table 1 summarises the assumptions and results that are obtained when we take the net income yield and assumed illiquidity premia as known and vary the assumed house price volatility in order to reconcile the ERM value at origination with the loan amount.
Table 1: Results summary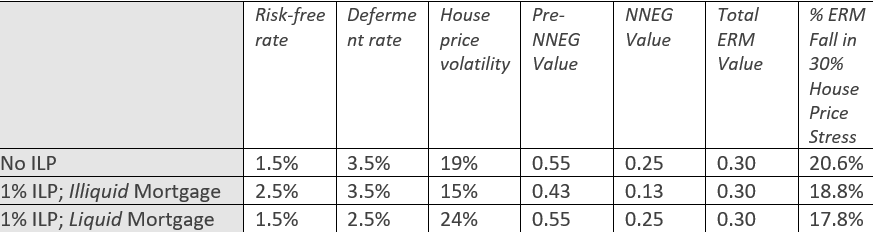
These results are consistent with Chart 2 above: when a positive illiquidity premium exists, its effect is to negatively impact on the value of illiquid mortgages and positively impact on the value of liquid mortgages. At origination, the mortgage value is anchored to the loan amount. Risk reduces the mortgage value. If illiquidity reduces the mortgage value, it implies less of an allowance for risk (volatility) is required in order to recover the same origination value. Likewise, if liquidity increases the mortgage value, a greater allowance for risk (volatility) is required to reconcile with the loan amount at origination.
In all three cases, we obtain a mortgage value at origination that reconciles with the loan amount. However, they do so by attaching different values to the pre-NNEG and NNEG components of the mortgage value. At origination, Case 1 (no ILP) and Case 3 (1% ILP; liquid mortgage) must produce the same NNEG value (because they must produce the same pre-NNEG value), whereas Case 2 (1% ILP; illiquid mortgage) produces a much lower NNEG value (because it produces a much lower pre-NNEG value).
The three valuation bases also imply different valuation sensitivities to future house price changes. In the examples above, in the ‘no illiquidity premium’ case a 30% house price fall results in a 20.6% fall in ERM value; whereas the same stress produces ERM value falls of 18.8% and 17.8% for the illiquid and liquid mortgages respectively in the presence of 1% illiquidity premia. Intuition for these different house price sensitivities can be found by considering the gradient of the lines of Chart 2 around the 30% LTV level.
Footnotes
[1] We may note that, under this definition of liquidity / illiquidity, a standard equity release mortgage asset would not be classed as liquid. In taking the mortgage, the house owner has raised cash by selling the (contingent) deferred right to possession of the house. The liability counterparty (i.e. the mortgage lender) does not have the right to demand cash settlement of the mortgage at any time prior to maturity (though the borrower may have such a prepayment option), and the mortgage would therefore be an illiquid asset by the definition developed here. The analysis of liquidity / illiquidity here has not considered how the ability to sell the asset to a third party may affect the definition of liquidity, and this is clearly a potentially significant limitation of this analysis.

No Comments