11 Dec 2020 On the Volatility of the Value of Deferred Possession

The value of an equity release mortgage is naturally a function of the value of deferred possession of the house that is provided as mortgage collateral. The mortgage value is also a function of the volatility of the value of deferred possession. Actuaries usually equate their estimate of the volatility of the value of deferred possession with their estimate of the volatility of the ‘spot’ asset value, i.e. the underlying house price. This short note briefly considers the theoretical behaviour of the deferment asset value relative to the spot value, and what this implies for its volatility. This analysis is intended to provide insights that may be useful in the calibration of equity release mortgage valuation models and in the calibration of mortgage capital stresses.

The basic relationship between the value of the ‘spot’ asset and the value of deferred possession of the asset

Suppose we have an asset, with market value S(t) at time t, and another asset exists that provides possession of that same asset, but with possession deferred to some later fixed future time T.

It is well known that the value of the deferred possession, D(t,T), can be determined by bifurcating the income generated by the underlying asset into two components:

The value of the spot asset at time t is equal to the market value of asset income receivable between t and T plus the market value of the asset income receivable after time T.

This tautology is helpful because the value of deferred possession is equal to the market value of the income receivable after time T. As a result, we can write the current value of deferred possession as:

D(t,T) is equal to S(t) less the market value of asset income receivable between t and T                  (1)

If the asset, S, pays a continuous income stream that is a constant percentage of the market value of S, then we can write:

D(t,T) = S(t).exp[-d(T-t)]                                                                                 (2)

where d is the asset’s net income yield. In this setting, d is often referred to as the deferment rate.

The above relationships suggest that changes in the value of deferred possession can arise from two distinct sources (or, more commonly, a combination of the two): changes in the ‘spot’ asset value, S(t); or changes in the bifurcation of the spot asset’s value between the value of the asset income receivable between t and T the asset income receivable after time T (which, in the simple special case above in (2), corresponds to a change in d, the asset’s net income yield). This suggests the value of deferred possession must be at least as (proportionally) volatile as the spot asset, and, to the extent this second source of risk exists in the particular asset cashflows of the given underlying asset, the deferred possession asset value will be more volatile than the spot asset value. Put simply, the value of the asset providing deferred possession has a source of volatility that the spot asset value does not: the value of the deferment asset is sensitive to changes in the net income yield (deferment rate) of the underlying asset, as well as to changes in the value of the underlying asset.

This discussion gives rise to some natural questions:

What behaviour in the spot asset price process determines whether the deferment asset will be more volatile than the spot asset? How different can the volatility of the spot asset and the deferment asset be? And does this vary with the length of the deferment period?

It is not the intended purpose of this note to provide empirically-determined quantitative answers to these questions for property assets. But a simple valuation model may help to provide some insights into what determines the answers.

An illustrative model for examining the relative volatility of the value of deferred possession

Let’s develop a very crude valuation example to help elucidate the relative volatility dynamics of the spot asset and the asset delivering deferred possession of the asset.

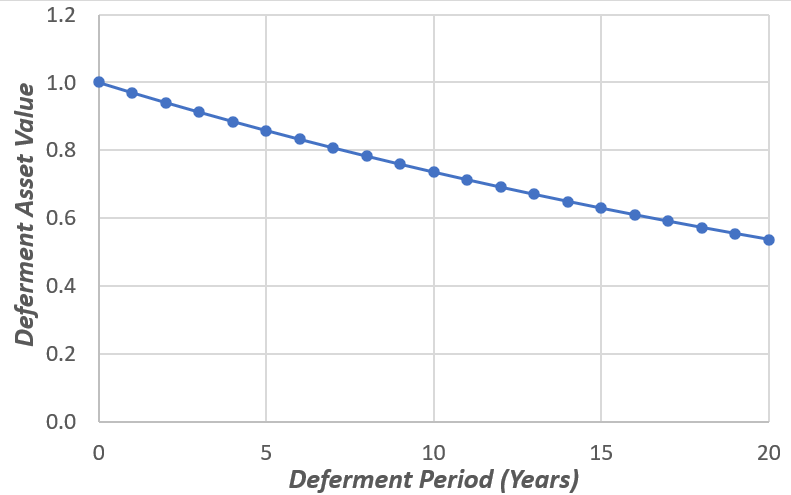
Suppose we have a property asset with a current price of 1. We value this asset as a discounted stream of expected future net rental cashflows. The expected year 1 cashflow is 0.03, the risk-free rate is 2%, the property risk premium is 4% and the net income is expected to grow at a rate of 3% in perpetuity. This valuation model provides a present value for the expected cashflow of the underlying asset at all future points in time (and the sum of those present values is 1, the current price of the asset). This valuation model therefore provides a valuation for the spot asset and the deferment asset for all deferment periods (using relationship (1) above).

Exhibit 1 shows the current values of the deferment asset as a function of the deferment period. In this simple example, the deferment rate for all deferment periods is equal to the asset income yield of 3%.

Exhibit 1: Current value of the deferment asset as a function of deferment period

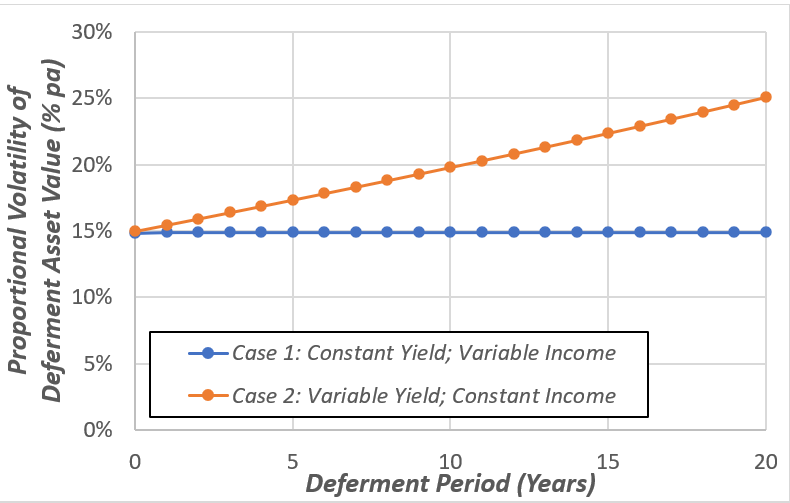
So far, this is all very simple and uninteresting! But now let us consider the volatility of the property asset value. Let’s suppose the property price volatility is 15%. What can we say about the volatility of the value of the deferment asset? The key point that arises from the above discussion is that this answer depends on what ‘causes’ the volatility of the spot asset value: in a nutshell, do changes in the spot asset value occur because the immediate net income of the property may materially change? Or because the income yield of the property asset may change? Doubtless, it will usually be a bit of both. But let’s consider the implications for the behaviour of the volatility of the deferment asset in each of the two limiting cases where all of the 15% asset price volatility is caused by only one of these two sources (change in income; change in yield).

Case 1: Constant income yield; variable income

Suppose the spot asset value only ever changes in response to changes in this year’s underlying asset net income; the expected subsequent growth of the income and its riskiness never changes. This is equivalent to saying the asset yield (and the deferment rate) is always constant.

So, let’s suppose the year 1 cashflow of 0.030 has a proportional volatility of 15%, and no other valuation parameter ever changes. In this case, the present values of all future asset cashflows vary by the same proportion, i.e. 15%. So, a change in the year 1 cashflow has the same proportionate valuation impact on all deferment asset values as it has on the spot asset value. The volatility of the spot asset is 15% and the (proportional) volatility of the deferment asset is also 15% for all deferment periods.

Case 2: Variable income yield; constant income

Now suppose the year 1 net rental income is known with certainty, and it is changes in the expected future growth rate of the net rental income that drives the spot asset value volatility. In this case, the asset yield will be volatile – an upward increase in growth expectations will result in a lower asset yield and vice versa. Suppose the expected growth rate of 3% has a (absolute) volatility of, say, 0.43%. That is, at the end of the year, the growth rate we assume in the valuation model is normally distributed around 3% with a standard deviation of 0.43%. This volatility in the valuation model’s growth rate assumption produces a volatility in the end-year spot property asset value of 15%. We can also re-value the deferment asset in every instance of the new valuation model, using the present value of cashflows produced by the model and relationship (1). Exhibit 2 shows the volatility that this variation in the valuation model produces for the deferment asset value as a function of the deferment period (these results have been produced using Monte-Carlo simulations, there are no doubt more elegant solutions available!).

Exhibit 2: Volatility of the deferment asset as a function of deferment period

As the deferral period tends to zero (i.e. T tends to t in the above terminology), the value of the deferred asset tends to the value of the spot asset, and the volatility of the asset providing deferred possession must therefore tend to the volatility of the spot asset. This is a general ‘boundary condition’: it is the case irrespective of the source of volatility in the spot asset price. But as the deferment period increases, the volatility of the deferment asset crucially depends on what is driving the spot rate volatility, and how it impacts on the bifurcation of the underlying asset’s cashflows between pre and post the deferment period. If the asset yield is volatile, the deferment asset will be more volatile than the spot asset. Put another way, this is simply saying that the deferment rate of the asset is volatile when the net income yield of the asset is volatile, and the deferment asset’s volatility is comprised of both spot asset volatility and deferment rate volatility.

It might well be argued that the above crude valuation model provides an unrealistic description of how the deferment asset volatility is likely to change as a function of deferment period. Most obviously, the annualised growth rate for very long-term income is likely to be less volatile than the near-term growth rate. This would, no doubt, be a reasonable argument. This model is not intended to provide a realistic description of how the volatility of the deferment asset changes with deferment period – our ambition here is much more modest. We are merely attempting to demonstrate that the volatility of the deferment asset price crucially depends on the volatility of the asset income yield as well as the volatility of the spot asset price. The results of the two cases above might be interpreted as bounds for what the volatility of a deferment asset can be when the underlying asset has a volatility of 15%.

So what?

This analysis may be useful when considering two distinct but related topics:

• The calibration of the property asset volatility in an ERM valuation model. In ERM valuation, it is the volatility of the deferment asset that matters, not the volatility of the spot asset. This analysis highlights that these quantities can materially differ. This ought to be taken into account in a calibration process that uses historical spot price volatility[1].

• The assessment of ERM capital requirements requires assumptions about the stressed values of underlying property prices, stressed values of deferment rates and their correlation. This process would arguably be simpler if we simply stressed the deferment asset prices instead of the ‘spot’ asset prices. This would remove the need for a separate deferment rate stress and it would remove the need for a correlation assumption between the spot asset and the deferment rate stress. With this approach, however, the stressing of the deferment asset would be based on the volatility of the deferment asset rather than that of the spot asset, and this too must be estimated with reference to the volatility of the asset’s income yield (deferment rate) and its correlation with asset prices.

[1] In my July 2020 research report on ERM valuation methodology, I argue for a valuation process that does not use historical price data to calibrate the house price volatility assumption, but I instead advocate calibrating the volatility process to observable ERM origination prices. It should be noted in the context of this discussion that this process technically produces a calibrated stochastic process for deferred possession assets, rather than the underlying house prices.